Calibration is the process of finding simulator input values for a historical time period which reproduce the observed simulator outputs over that period. To accomplish this a distinct calibrator framework is created alongside the simulator framework, within the same model family (see How it's Organized). There are two main motivations for calibration. The first is to look back at the history of a system through the same conceptual framework used to explore the future of that system - a prerequisite for trend analysis. The second is to get starting values - or initial conditions - of model stocks.

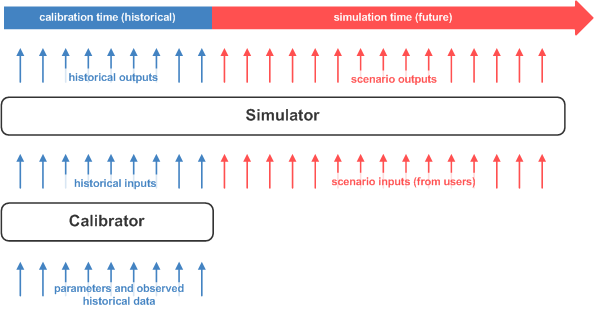
The diagram above shows the relationship between a simulator framework and its corresponding calibrator framework - with respect to inputs, outputs and the time periods for which they operate. Key points to note:

• The simulator contains logic that transforms input variables to output variables, and this same logic is applied for future simulation (pink time period) and historical calibration (blue time period).
• A major difference between the simulator being run for future simulation vs. historical time has to do with the source of the inputs. For future simulation the inputs originate from the model users. Different input sets give rise to different scenarios. For historical time, however, the simulator inputs are produced by the calibrator framework whose job it is to ensure that simulator outputs match observed historical data. The calibrator logic is only exercised over historical time.
• Observed historical data, together with calibration parameters, are taken by the calibrator and used to calculate historical inputs - and in turn historical outputs - that best represent historical trajectory of modelled system.

As an example, take a simple population model in which

population_t = population_t-1 + net immigration_t-1 + births_t-1 - deaths_t-1

If historical data for population, births and deaths are available then calibration involves determining the historical net immigration levels. For real-world models this is a non-trivial problem and requires a separate calibrator framework because:

• Simulators are dynamic and data-rich; they contain many inter-related, multidimensional time-series variables which constrain the calibration solution. In the example above the population variable, rather than being a vector, might be a 3-dimensional variable stratified by sex, age and time.
• Simulator variables in historical time may not be directly measured and therefore may have to be estimated, and/or there may be missing periods of observed data which require interpolation. For the population model example it is common to use a simulation time-step of 1 year, and while births and deaths data may be available for each year, population census count data is more likely to be collected every 5 or 10 years. The calibrator must deal with the varying temporal resolution of the datasets.
• Data quality issues are common, and often manifest themselves through inconsistent or infeasible calibration results. For example, suppose that net immigration in the above example were broken into its component parts - immigration and emigration. If estimates for historical immigration were available and used in the calibration to estimate emigration levels, it is possible that a naive calibration procedure would produce some negative values for historical emigration. Of course, this is infeasible and so the calibration framework must consider these issues to produce an internally consistent and feasible calibration solution.

Note that the term calibration used in the whatIf? Platform (Design Approach) context differs from specification and estimation of a statistical model. In particular, the use of data is different as in statistical modelling the data are used to estimate the parameters in the model using an appropriate statistical technique, while in the design approach, data which have not been measured, such as lifetimes of capital stocks, are estimated and then the data set is used to calibrate the model. The calibration is successful if the model reproduces the data, given a set of historical input variables, and this is considered a necessary but not sufficient condition for a valid model¹⁾.